Kalman Filter Localization

Learning some about probabilistic robotics, specifically Kalman Filters for state estimation!

Kalman Filter Demonstration

Abstract

This semester I worked through the book Probabilistic Robotics to expand my knowledge in robotics algorithms. I learned about various statistical techniques used for the localization of mobile robots. While I originally planned to implement the mentioned algorithms in ROS2 in simulation, that proved to be a larger task that wasn’t suited to my semester plan. I have instead implemented a 2d Kalman Filter for state estimation in a simulation I built enturely myself. This project is captured in the rest of this page.

Goals

• Learn C++
• Actually understand what each step of the Kalman filter is doing
• Understand the limits of the Kalman Filter (and its derivatives)

Understanding the Kalman Filter

The Kalman filter is an extension of a Bayes Filter. It is a recursive state estimator, it uses information about the previous state and some measurement to infer what the new current state is! The Kalman filter is more useful than Bayes filter in many robotics applications because it is computationally not possible/scalable to calculate some of the required values in a Bayes filter for large state spaces.

A Kalman Filter derivation can be found here for anyone curious. Notably, everything in the Kalman Filter is a Gaussian distribution so our predicted states have means and covariances.

The Kalman Filter can be thought of in 2 steps: the prediction step, and the update step. The prediction step uses prior information to get a best guess estimation of the state. This estimation is then used in addition to a measurement to determine how far off we are from where our measurement says we should be. This metric is used to determine a “best fit” state between our measurement and state prediction. Note that this is powerful because we can model the uncertainty of our prediction model and our measurement model separately so we can take “trust” different parts of our system differently. Imagine a robot with bad encoders but a fancy lidar system that gave you a position estimate – the kalman filter would allow us to reconcile those different amounts of error and weight our state estimation closer to the “lidar” state.

Now lets see some of the math!

Kalman Filter Prediction Step

Shown above is the prediction step of the Kalman filter. This step incorporates the perceived control command and updates the uncertainty of this prediction(the covariance).

Kalman Filter Measurement/Update Step

Next the measurement/update steps are implemented. This is shown in the above figure. This compares the true measurement to what we expected to measure given our predicted state. The next lines determine the Kalman Gain, a weighting of whether our measurement or motion model is more accurate, to choose the final predicted state somewhere between the measurement and the motion predicted state. This step removes uncertainty and shrinks the size of the covariance matrix.

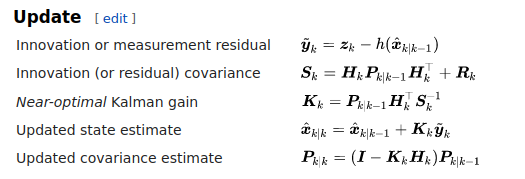
Implementation

I implement a simple Extended Kalman Filter in C++ to get a better understanding of them. I decided to write my implementation in C++ to challenge myself in a new language. I made use of the Eigen and SDL2 libraries to implement matrices and graphics.

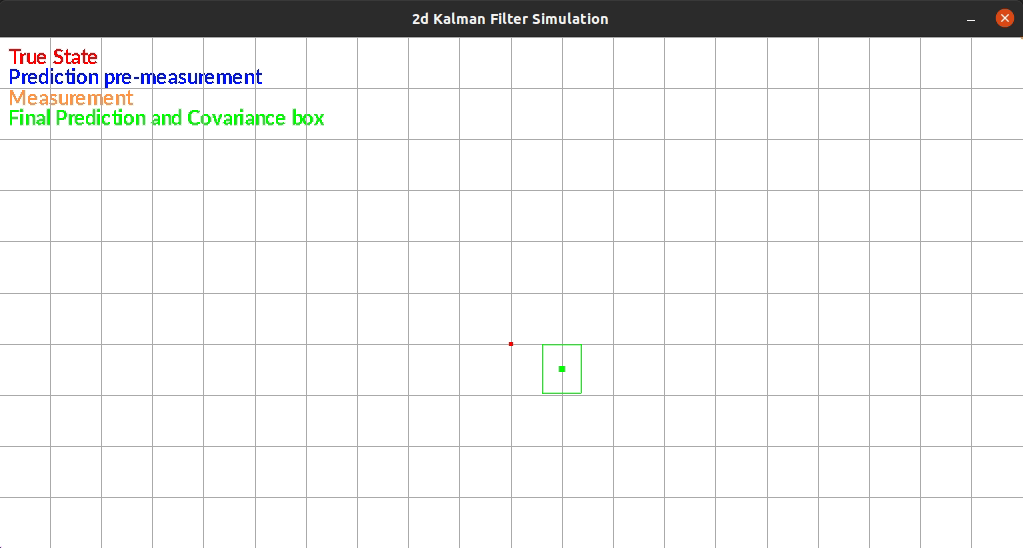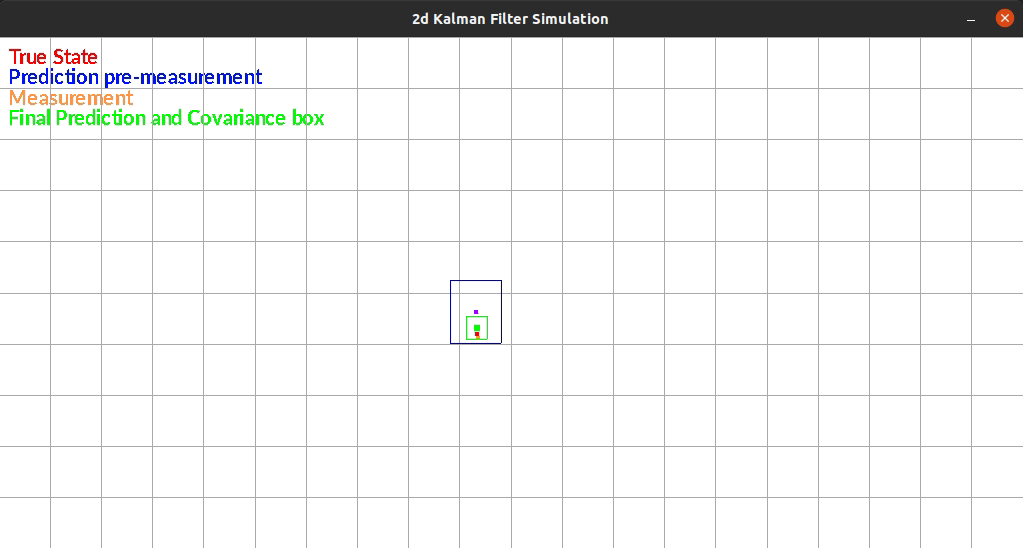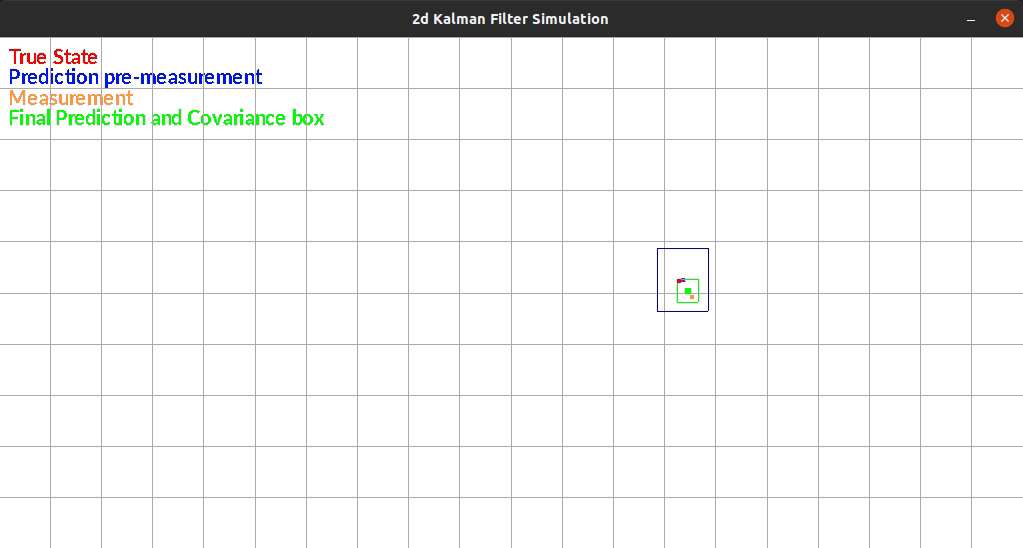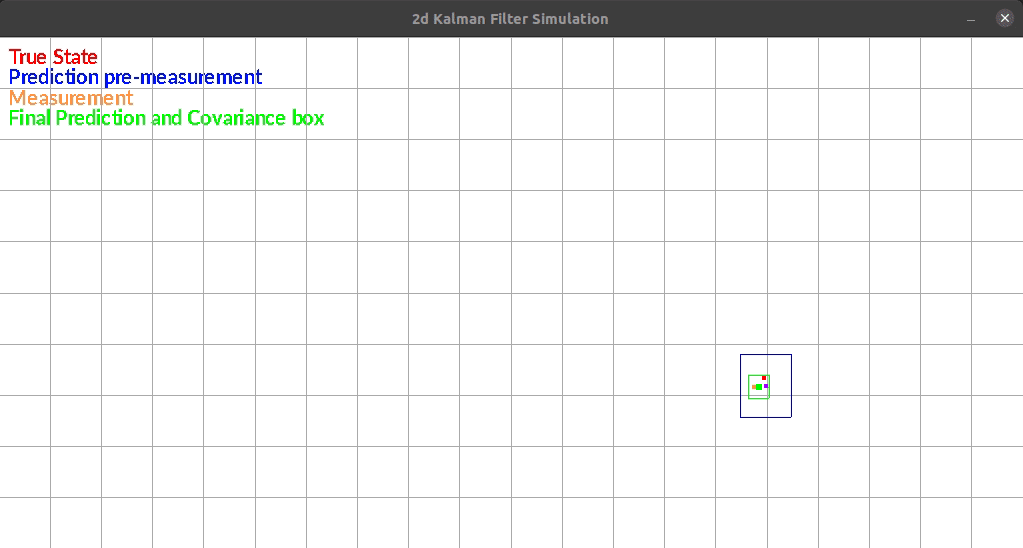
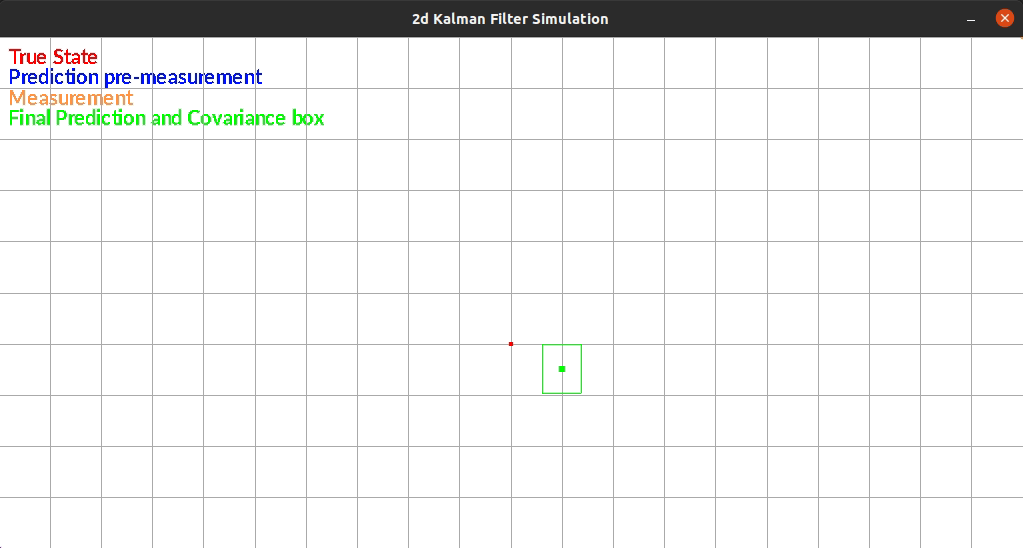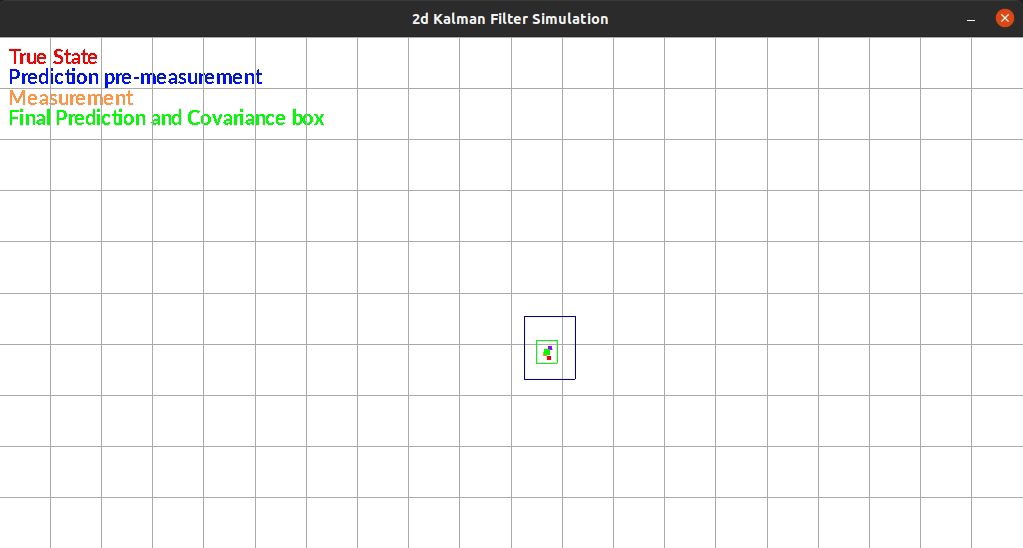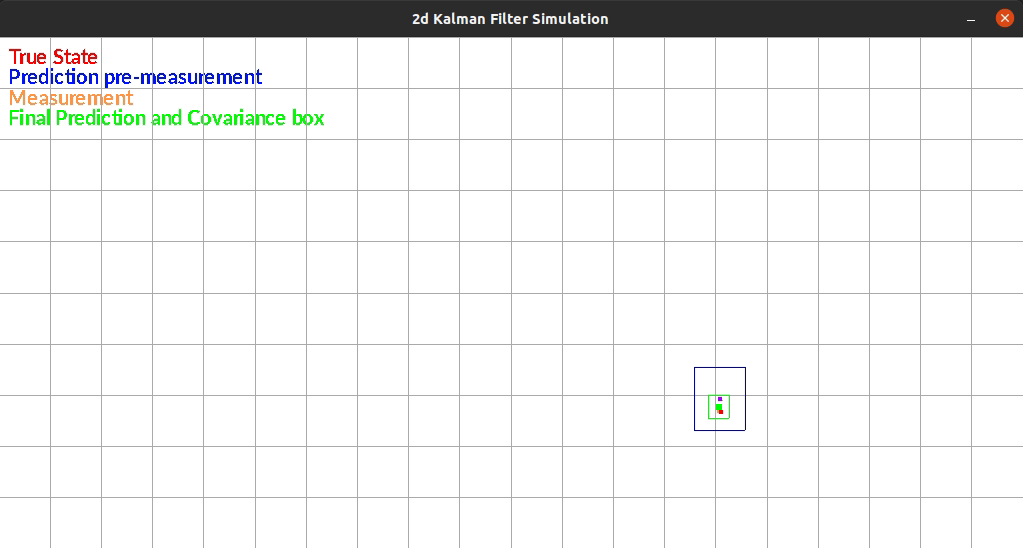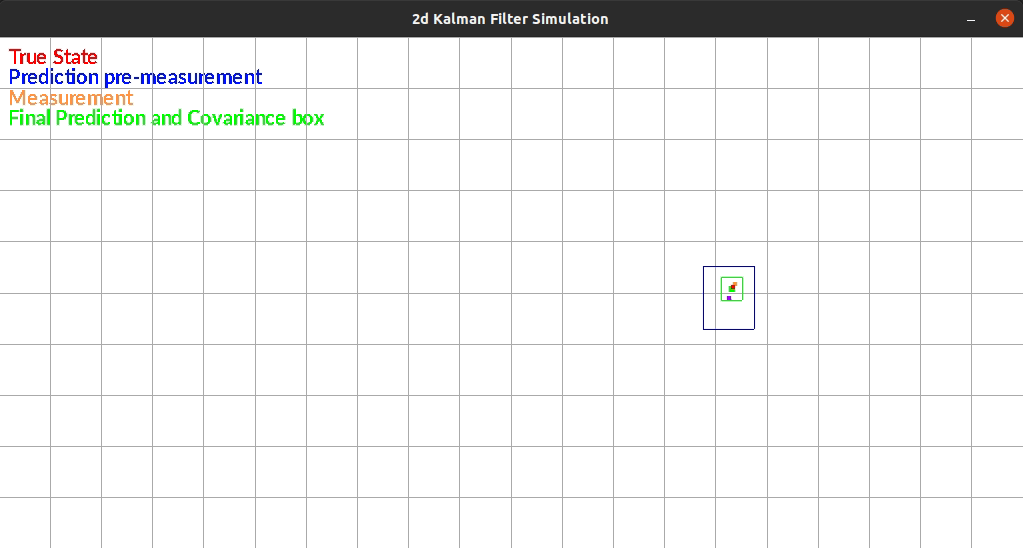
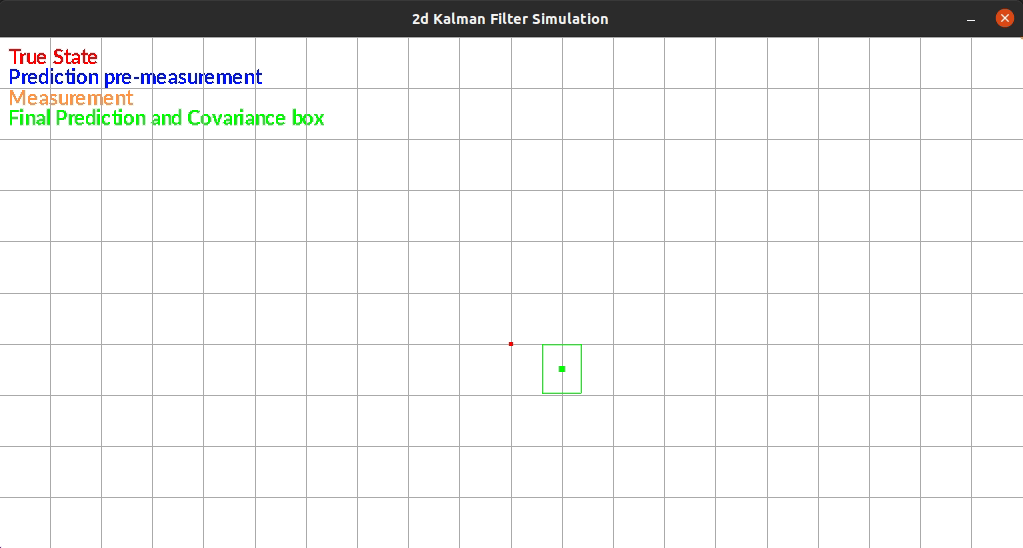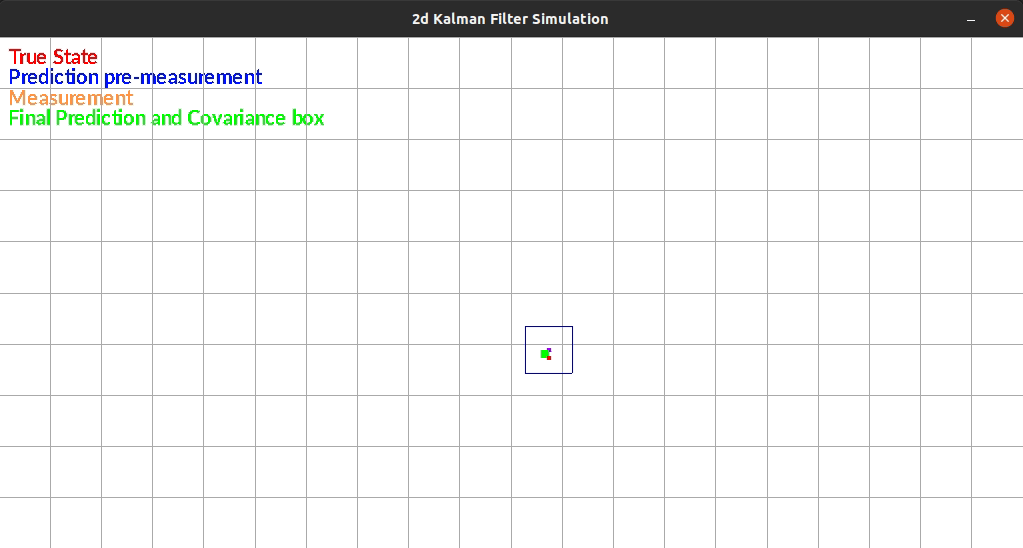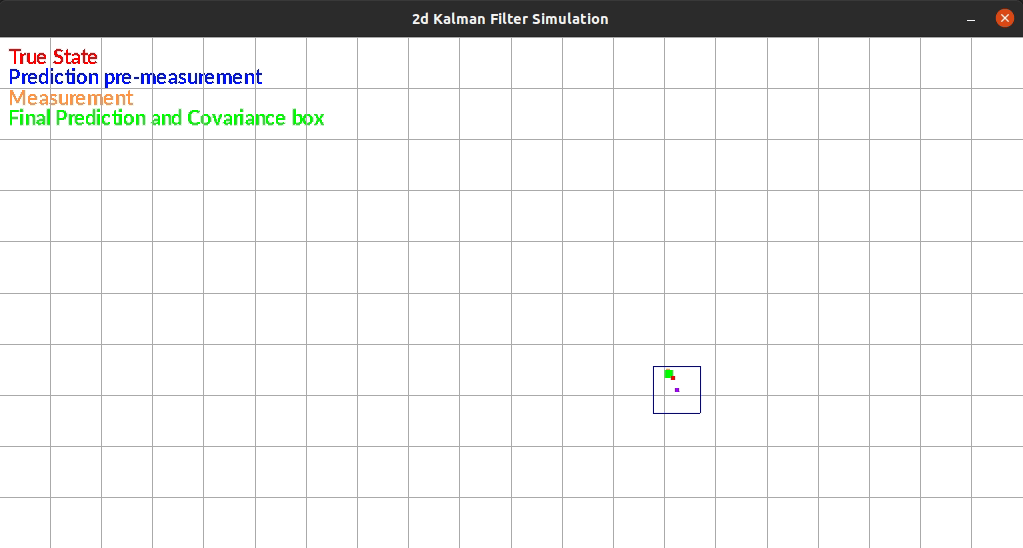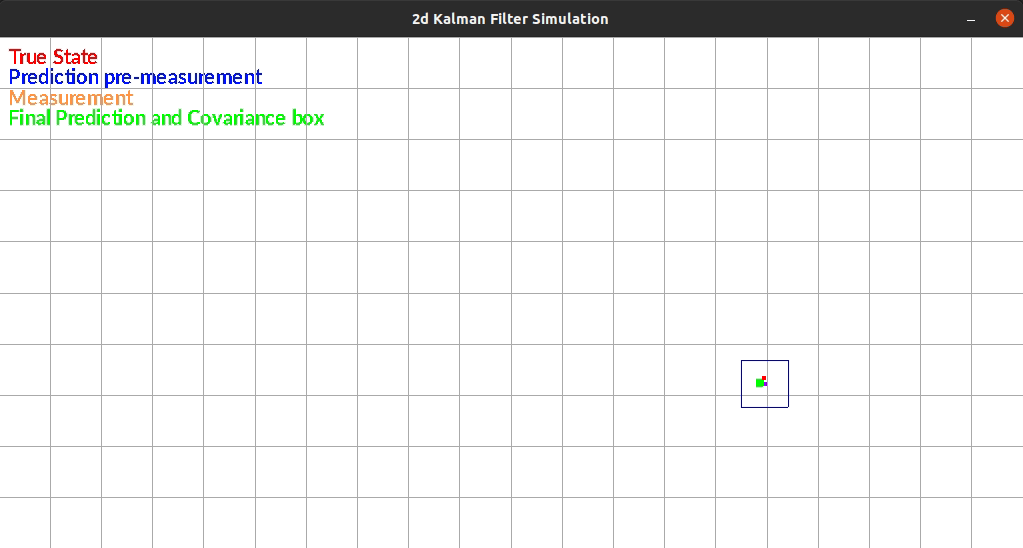
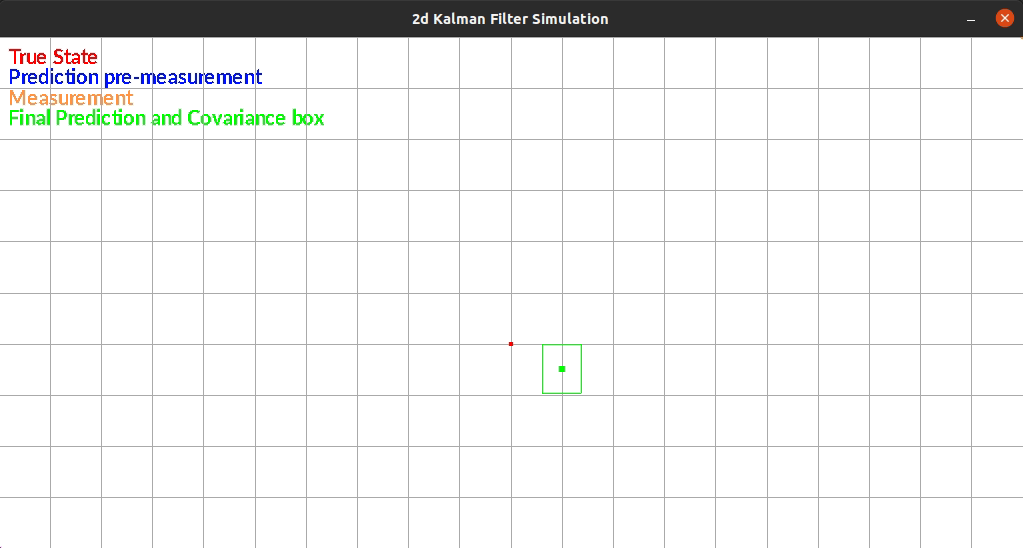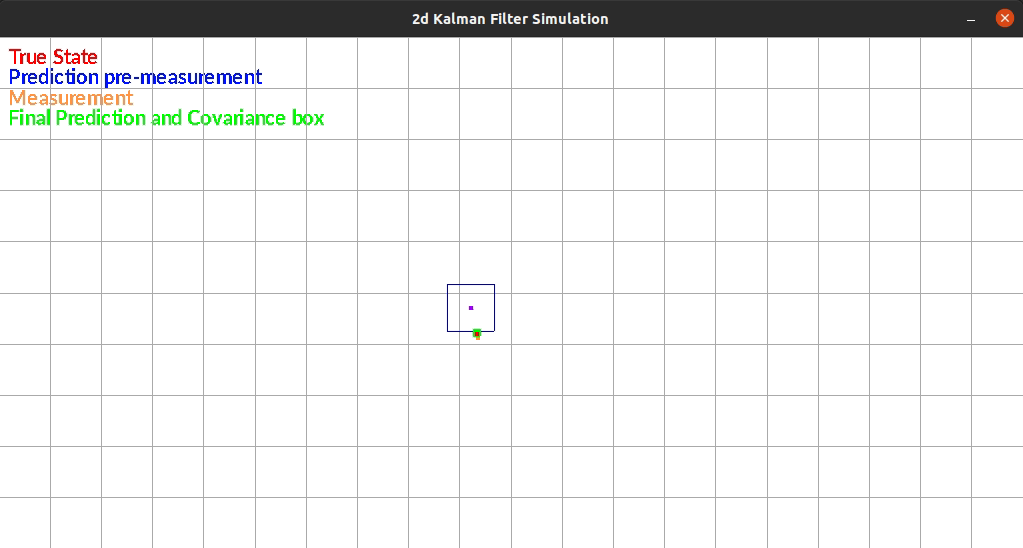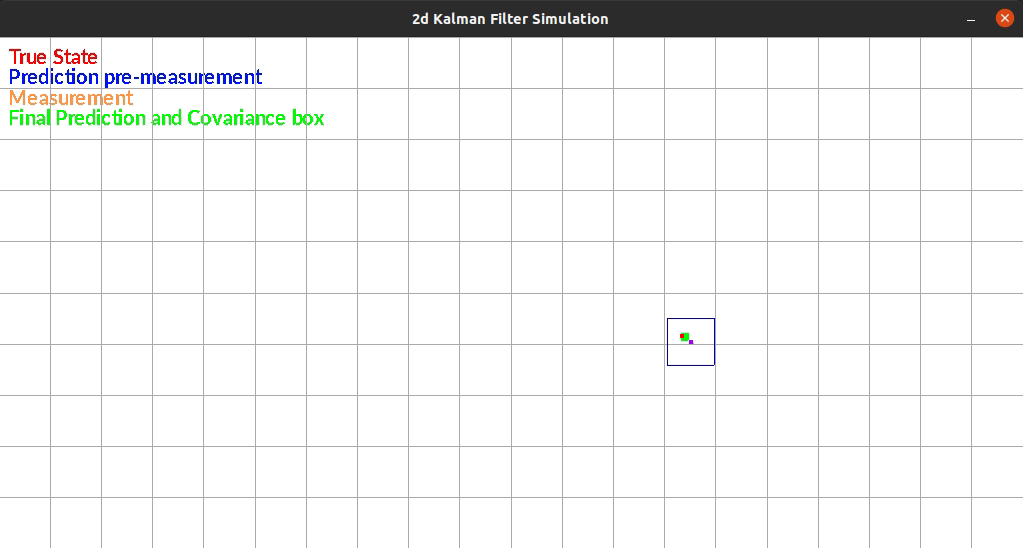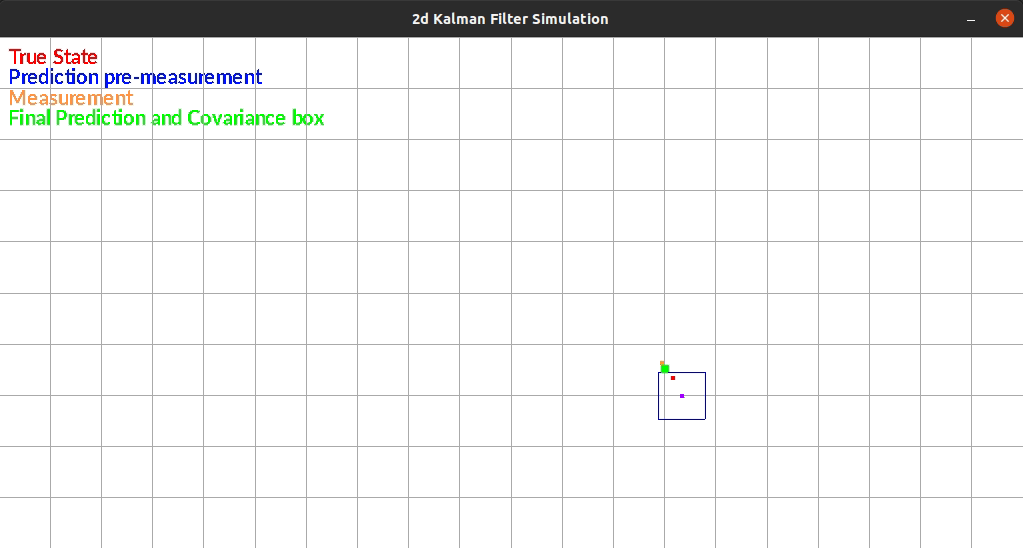
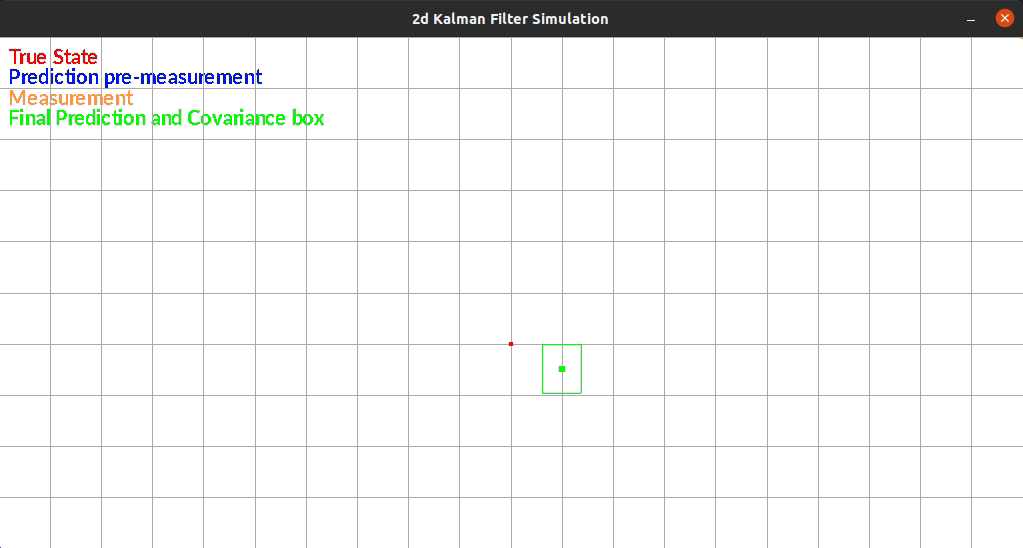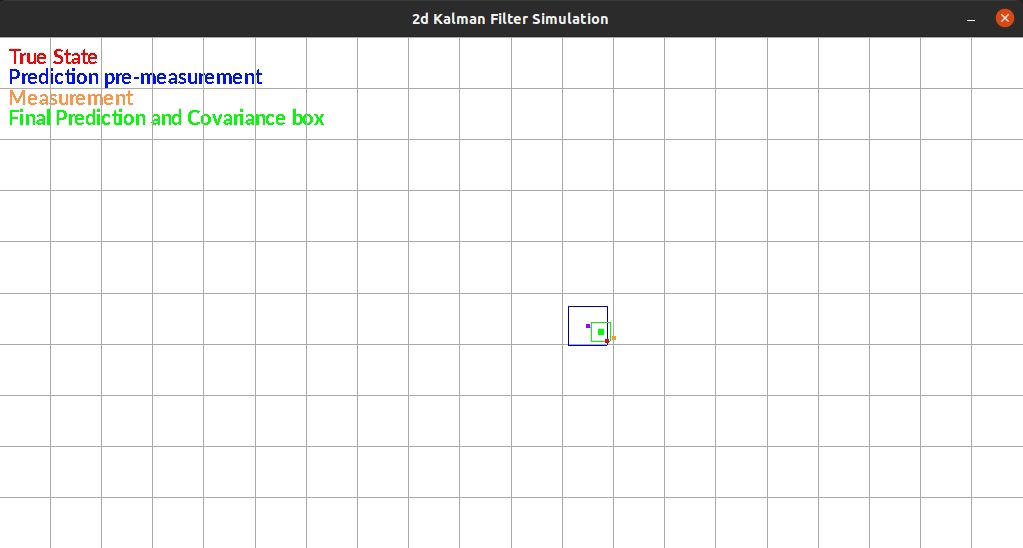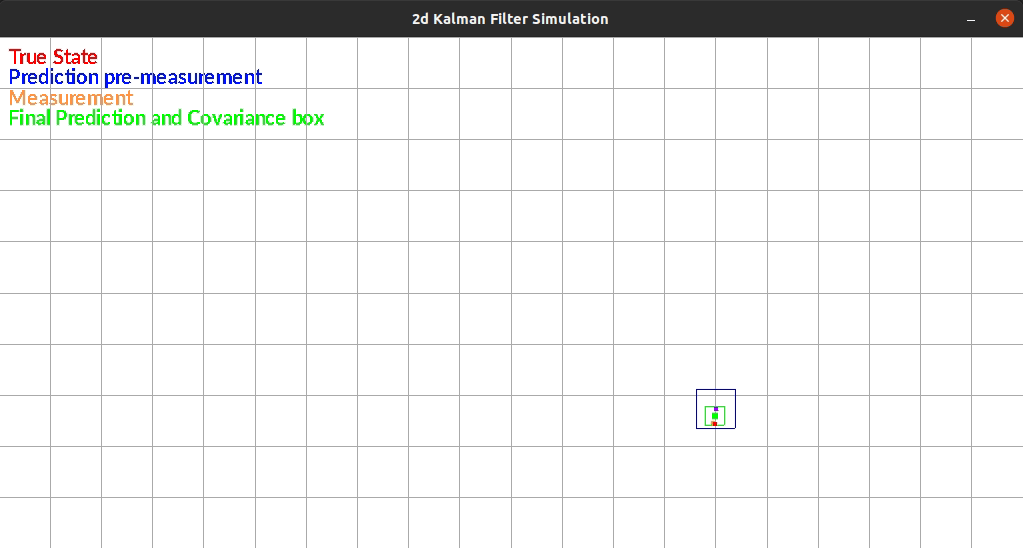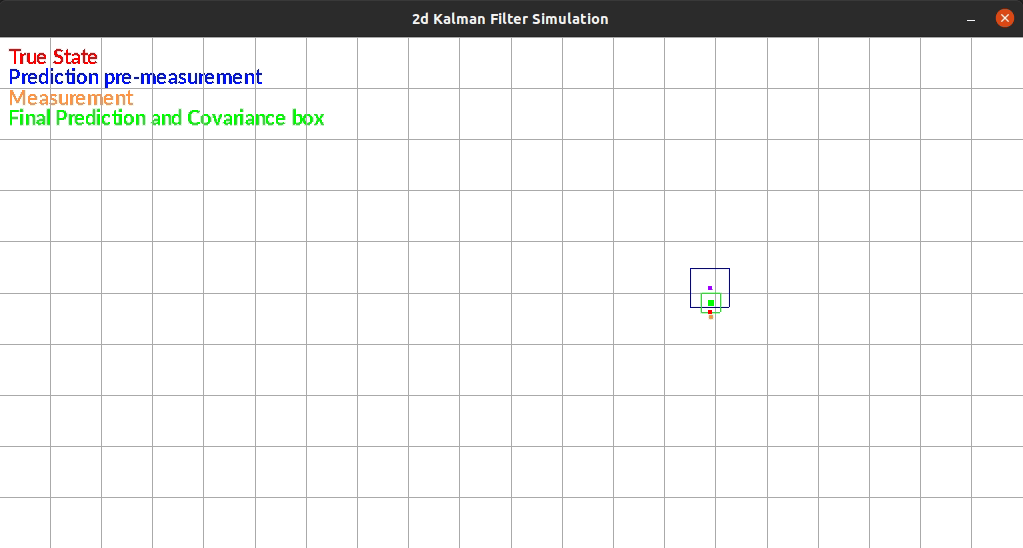
The Kalman Filter I wrote estimates position in a 2d grid. The “robot” has sensors that sense the walls to the left and right of it. The robot is constrained rotationally. It also has encoders such that it can estimate it’s position based on control commands.

The robot currently exists in a box and moves randomly each timestep. There is additive gaussian noise to the original movement, the measurement of the walls. One limitation of my system is that noise is the same distribution regardless of the movement or size of the movement. This makes small movements extremely noisy since the error can be as large as the movement itself.

The figure below shows an example run of the system. It moves randomly and you can see it corrects back towards the true estimated position even after it gets off.

Kalman Filter Demonstration

I tried simulating this system with different amounts of noise in the measurements and positions, as well as differing covariances that modeled their uncertainty.

Kalman Filter with very accurate measurements, note the orange dot is almost always closer to the true position than the blue

Kalman Filter accounting for this very accurate measurement, note how final state is usually on top of measurement

Kalman Filter trusting the measurement too much (measurement is noisy compared to movement and not accounted for)

Kalman Filter trusting the movement too much (movement is noisy compared to measurement and not accounted for)

Reflection

Reading through Probabilistic Robotics was hard! I have some gaps in my probability knowledge. With that said, I gained a lot of background and strategies to think about how robotics systems and algorithms can operate. I have a much deeper understanding of the Kalman filter the before and understand the pros and cons of several different state estimation methods.

It was really interesting to see how the Kalman filter is actually kind of hard to implement for many applications.The requirement for things to be linear is quite difficult and then to remedy this you must approximate things as linear. The Extended Kalman Filter requires a Jacobian to be calculated for the measurement and prediction models which also adds complexity for complex states. Seeing these limitations has been insightful and has made me more curious about how a particle filter can be used as well as doing SLAM with particle filters.

What I want to learn next!

I am really interested in moving past state estimation with Kalman Filters – I want to learn more about how particle filters are used for large state spaces. I’m also really interested in mapping and then navigation within mapping. I’m excited to explore more about these topics, maybe even on real hardware!

References

16.4 Extended Kalman Filter - 16.4_Extended_Kalman_Filter.pdf

Localization strategies for autonomous mobile robots: A review - ScienceDirect

Particle Filter Localization with Webots and ROS2 | by Debby Nirwan | Towards Data Science