Abstract
Course Project to build and implement a Particle Filter using Lidar data and existing maps. Done in simulation in python.

Goals
The goal of this project was to implement a particle filter algorithm in the context of robot localization. Our primary focus throughout the entire project was learning: we wanted to write as much of the code ourselves as possible and understand the components of the codebase that we didn’t author. Our secondary goal was to have a useful particle filter that was powerful and accurate enough to be used in practice, and to incorporate some interesting experimental features along the way.
What is a particle filter and why do we use it in the context of robot localization?
The objective of our software is to localize (or locate) our robot within a known physical context. In other words, using current robot sensor data and past motor movements (along with the associated probabilistic robot sensor and motor models), and using a map of the overall space, we seek to predict the robot’s current state - or it’s position in physical space.
The naive approach to localization is via a discrete Bayes filter - here, we know there are n discrete states (or positions & orientations) our robot could be in. For every time step t, we simply compute the probability of our robot being in each one of these states, and pick the highest one. We’ll figure out, with a little math, that the time complexity of this computation is a simple O(N^2) - (AKA it’s really slow).
We can take a few steps to shave this process down and save ourselves some pain. What if, instead of computing the probability of our robot being in every single state, we only computed the probability for a select group of states that’s more relevant? What if we used the robot’s sensor data and motor data to inform these possible states - and narrow them down even further?
We could consider each possible state (we’ll call these particles from now on) to be a possible robot position, and we could compare the robot’s current scan data with each particle, superimposed on the known map. Now, we know the likelihood or viability that each particle is actually where the robot is!
As the robot moves through the map, we transpose each particle and recalculate weights based on the particle’s likelihood. Poor guesses at the robot’s position, or particles with lower weights, get cut out and resampled around the positions of particles with higher weights. Ultimately, as the process continues the robot is exposed to more surroundings that help its particles converge to an accurate representation of its position.
An overview of our implementation
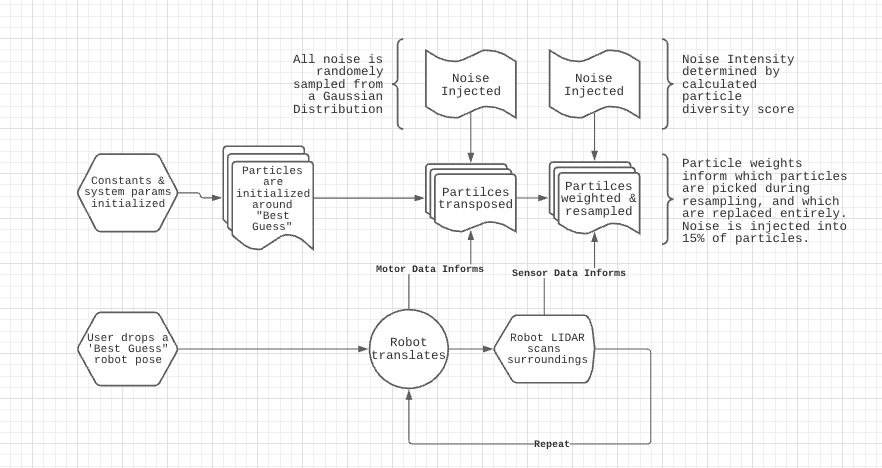
The implementation of our particle filter can be broken down into several steps that get repeated throughout time. Below is a block diagram & high level explanation how we specifically applied the filter.
Some specifics of our setup
- Using ROS (Robot Operating System), RVIZ, and Python’s ROS API to interact with a simulated NEATO robot
- Using the Neato’s default LIDAR scan data on the ROS /scan topic for sensor data, publishing our particles to the /particlecloud topic, and driving the Neato via the /cmd_vel topic
Algorithm Walkthrough
Setup
Start by initializing system constants and parameters Require user to drop a “best geuss” of the Neato’s starting position. Create an initial particle set around that “best guess” pose.
As the robot moves
- Map the robot’s movement onto each particle as if the robot was at each particle’s position
- While translating particles, add noise to compensate for the robot’s odometry measurements - (the robot’s motor model and onboard encoders aren’t perfect)
- Scan the surroundings with the LIDAR sensor
- Project the lidar scan as if it were from each different particle pose
- Assign a weight to each particle based on how similar the mapped scan is to the ground truth “map”
- During particle resampling based off assigned weights, retain 85% of particles from the previous particle distribution, with their weights as probabilities of choice
- For the final 15%, sample from the same distribution, but inject noise for each particle position (this variability is key in the event that our current particles don’t reflect the robot’s position)
- If particles have condensed too much then add variability - we’ll cover this more in depth later! (This helps the particle filter continue to work as error accumulates)
- Repeat indefinetly!
As this process repeats the point cloud should converge onto the actual position of the robot. Changing parameters such as the amount of resampling done or the amount of noise injected changes how the particle filter behaves.
Here’s a few more clips of it in action! The large red arrow is the ground truth position of the robot. the small red arrows represent our particles, in theory if our filter is working they should stay relatively condensed arounf the larger red arrow. The white lines that move are the lidar scan of the robot superimposed onto the map.

Our core design decisions, explained
Running with pf.py
We chose the more sparse codebase over the scaffolded one offered to us, in the interest of learning from the ground up.
How we calculated weights
In order to quantify which partilces were ‘better guesses’ at the robot’s state than others, we set each particle’s weight using the Neato’s LIDAR scan data. This can by walking through all particles, and for each particle, walking through each of the robot’s LIDAR scan points projected to the particle’s frame. From there, project this onto the actual map and determine the distance from the nearest actual obstacle. Append each distance to an array, with 1 array for each particle.
Apply a Gaussian ‘squish’ to each point, cube the result, and sum the entire thing to calculate one particle’s weight (between 0 and 1). The result looks like sum([((e/(d)**2))**3 for d in array]). We settled on this weight calculation to heavily emphasize values of d closer to 0, and strongly diminish values of d higher than 1.
Using n_effective for dynamic noise injection
Let’s think about injecting noise into each particle during resmapling. How do you build a system that is aware of how varied or diverse its particles are, and one that can adjust how much noise it injects based on that ‘diversity score’? In other words, how do you make sure you don’t go in blind when injecting noise?
We use n_effective to store our calculated variance or diversity score of sorts. The more diverse our particles and the wider our spread, the better our system is at handling out of the ordinary edge cases - like if the robot were kicked, for example. (Note that we also want our particles to condense fairly well for an accurate best guess at the robot’s position).
To calculate n_effective, we sum the square of each particle weight, and divide the result by 1. It looks a bit like n_effective = 1 / sum([w**2 for w in weights]). This model for n_effective grants your filter a higher score for a more diverse set of (possibly shitty) weights, and a lower score for a lot of low scores and couple high scores.
When injecting noise, the standard deviation of the Guassian noise (reference numpy.random.normal) is proportional to 1/n_effective. This method has its downsides - it’s directly dependant on the number of particles in the system, and must be finely tuned depending on the context in order for it to not ‘over-prioritize’ variation in particle positions.
Challenges
In general, debugging the system came down to writing incremental bits of code / logic and testing as often as possible.
In particular, one significant challenge for us was keeping track of and jumping between the coordinate frames. The lidar scan, the robots in-built odometry, and the robot itself all live in different coordinate systems and must be transformed between. These are pretty tough to conceptualize. Luckily the tf module takes care of much of the work behind the scenes. This was likely the largest conceptual hurdle for us to overcome.
Later in the project, we faced some issues injecting noise and variability into our filter. Even after rooting out some simple bugs, we realized that setting an appropriate noise level and ensuring a reasonable variation in the particles was no small feat, and required a ridiculous amount of fine-tuning. It was very easy to come out with an overly or not aggressive particle filter. We eventually switched to the n_effective method, which isn’t perfect but is an improvement.
Improvements for the future
Obviously this particle filter leaves some to be desired. It works decently when given an accurate estimate and a clean map with time & patience to lock in its best guess of the robot’s state.
To improve performance, we’ve considered both some minor adjustments and bigger picture changes to our algorithm.
- Vary not only the noise, but the number of particles resampled based on the variance score
n_effective - Improve and tune in motor model/noise injection
- Experiment with higher and lower numbers of particles depending on map characteristics
- Optimize code for memory and time complexity to enable a faster timestep
- Detect if the particle cloud has diverged and work to resolve the divergence using clustering algorithms
- Experiment with a more versatile way of computing robot location than a weighted average of particle position The above changes are intended to be a list of ideas that warrant exploration rather than a prescribed set of instructions to a better filter.
Lessons Learned
- This was the first time we were forced to use bag files. This was extremely powerful and made testing 1000 percent faster. This is something we will carry on to future projects where applicable.
- Dividing work so that two people could be developing independently greatly increased our productivity. For example we would implement a calculation without adding noise, and then someone could work on the noise implementation and someone could work on the next calculation concurrently while still being able to test the code and avoid most merge conflicts.
- Systems quickly become too big for print statements! While we used print statements to track which case’s our code is transitioning to, visualizations or doing small tests to verify logic is a must.

